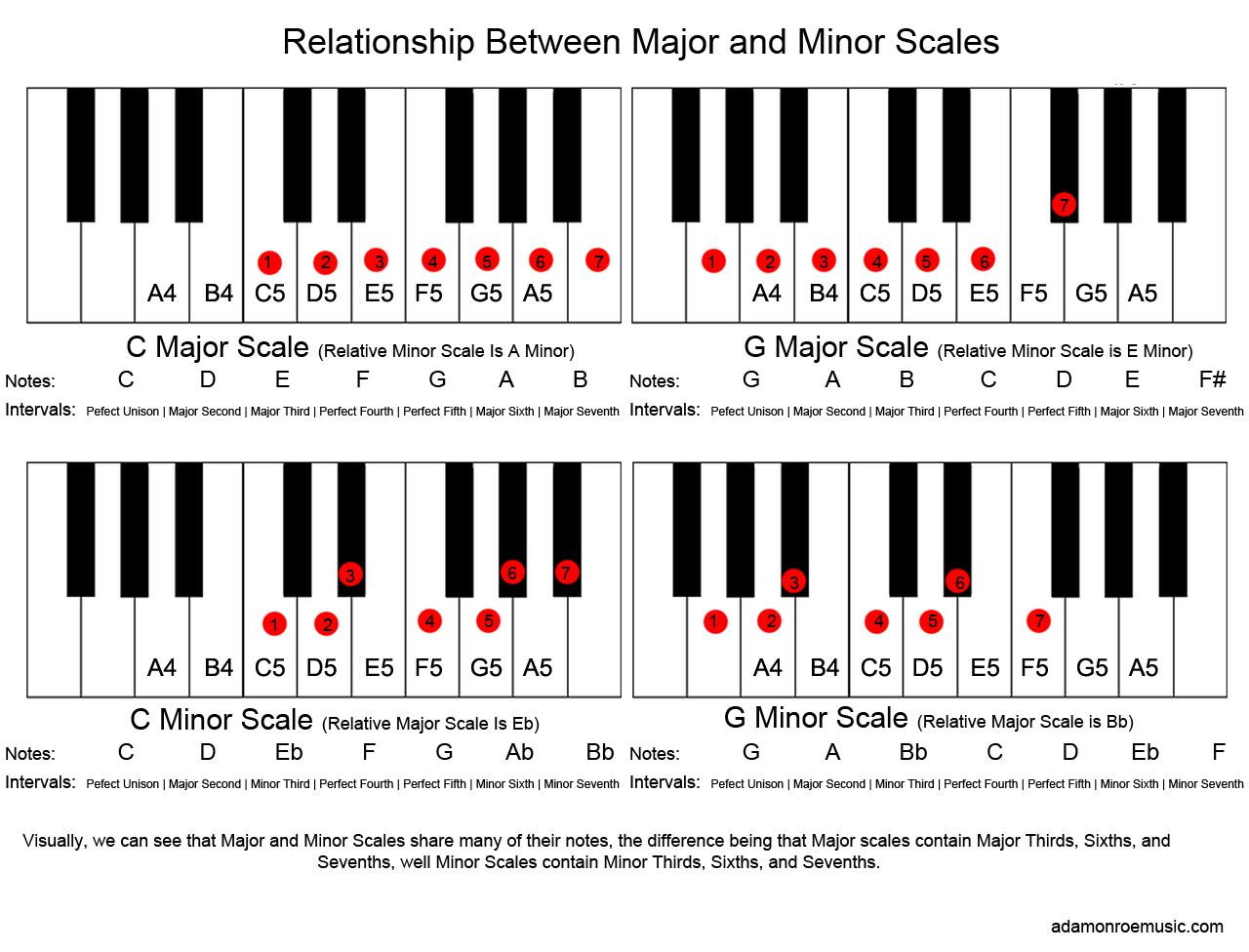In western music, there are two fundamental scales - the major and minor - from which are constructed the 24 major and minor scales. In music, a scale is a series of intervals that are repeated. Scales are repeating patterns, and thus it's common for people to learn major and minor scales in terms of whole-steps and half-steps (or whole-tones and semi-tones). In the case of music theory, it's more helpful to think of scales in terms of intervals. If we understand the differences between intervals, we can greater comprehend the difference between scales.

The twelve major scales are "constructed" the same way for each of the twelve-tones in western music. We begin with the root (or perfect unison), and add the perfect second, major third, perfect fourth, perfect fifth, major sixth, and major seventh, returning to the root an octave higher. This is equivalent to the pattern W-W-H-W-W-W-H where "W" and "H" represent whole-tones and semi-tones, and we begin with the interval of a perfect second, and end with the distance between the seventh and the root. In the Key of C Major, our major-scale notes are C, D, E, F, G, A, B. This is a seven-note diatonic scale.

The twelve minor scales are constructed much the same way, but with different intervals. The perfect second, perfect fourth, and perfect fifth remain the same, but we use the minor versions of the third, sixth, and seventh. Thus, the only difference between major and minor scales are the third, sixth, and seventh intervals. W-H-W-W-H-W-W.

One might ask themselves, "why use these specific intervals?" The answer is that we derive the notes diatonically from a series built on perfect fifths. We do not start on the root of the scale, but on the fourth. For example, in the key of C we have F-C-G-D-A-E-B. If we were to build fifths starting on C instead, we would get C E G D A E B F#. Likewise, in G we begin with C and and end up with the "natural" notes of C, but with F# as our seventh.

The minor scales are derived using the same method of stacking perfect fifths, because each minor scale has a relative major scale. Specifically, the minor third of every minor key is that key's relative major. Using C as an example, C's minor third is Eb, so the relative major key of C Minor is Eb, and thus the key of C Minor and Eb share their accidentals - Eb, Bb, and Ab. It is sometimes easier to think of minor scales/keys as different modes of the major scale. Indeed, you can derive many different scales (or modes) from the major scale by starting on different notes, not just the minor scale, and there are different names for each of these modes. The technical name for a major scale's relative minor scale is the Aeolian mode.

If we were forced to build major and minor scales every time we needed to determine what notes are contained within a key signature, we'd be faced with a never-ending, remedial task. Luckily, music has evolved as a hierarchical system of notation wherein we need only to remember what notes belong to a key, and really, we only need to remember the major keys, as minor keys share accidentals with their relative majors.

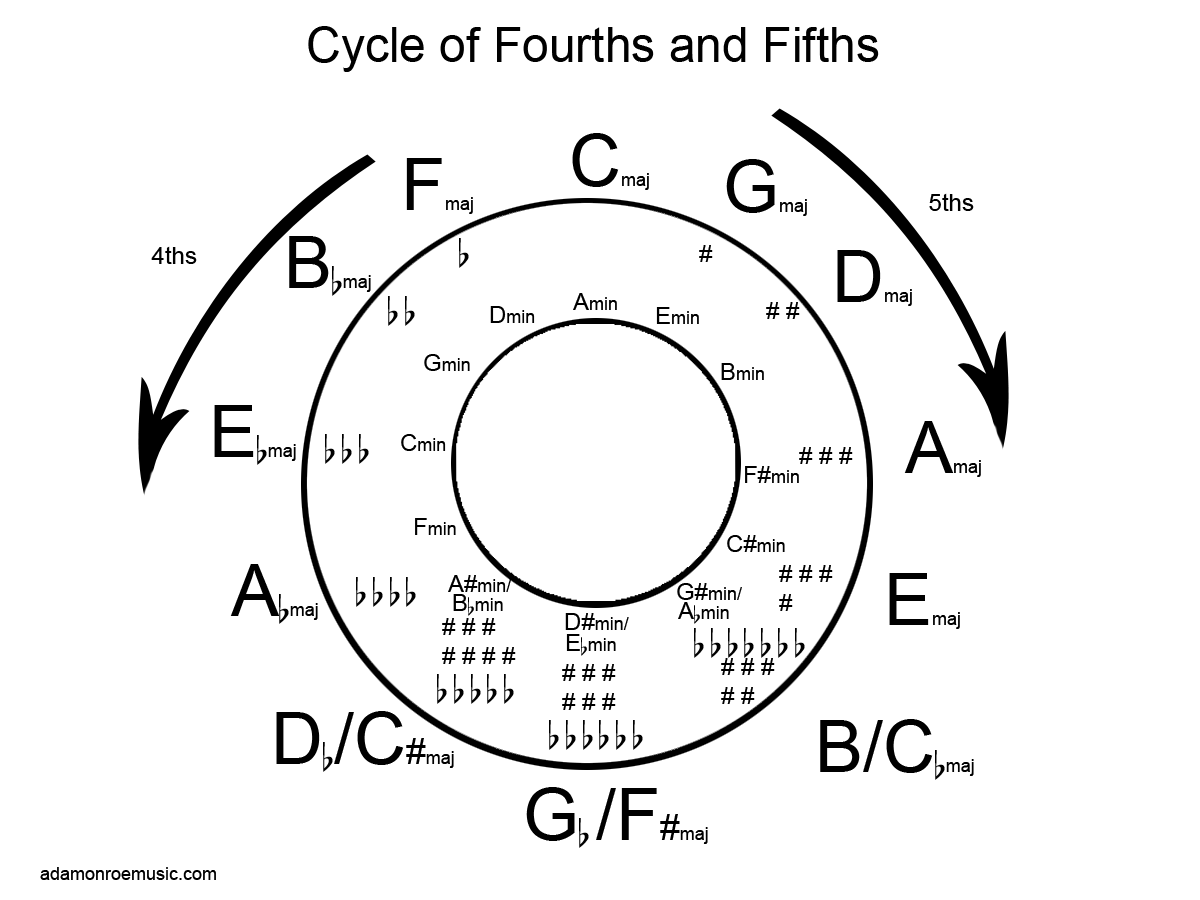
The Circle of Fifths is as follows: F-C-G-D-A-E-B. Look familiar? Using this pattern, we can easily remember all the major sharp keys. Read this pattern backwards and you'll get B-E-A-D-G-C-F; these are the accidentals for the major flat keys. Regarding the sharp keys, the first accidental is F# and belongs to the key of G. The next key is D, and contains the accidentals F# and C#. The next key is A, and contains the accidentals F#, C#, and G#. Following this pattern, we only need to remember the cycle of fifths - F-C-G-D-A-E-B, and that whatever note we choose to end on, the key signature will be the sharp form of that note plus a half-step. For example, using the accidentals F#, C#, G#, D#, and A# puts is in the key of B Major, leaving B and E as natural notes. The B major scale would then be B-C#-D#-E-F#-G#-A#.

Again, theCircle of Fourths is as follows: B-E-A-D-G-C-F. The trick to the flat keys is that each key contains the proceeding flat accidentals in the circle of fourths combined with the next accidental in the cycle. Therefore, the key of Bb contains not just Bb, but also Eb. The key of Eb contains the accidentals Bb, Eb, and Ab.

Constructing major key signatures in this way leaves C as an exception, having no flats or sharps. This method also generates a few redundant key signatures. There can only be 24 major and minor keys, two for each of the 12-tones in western music. Yet if we construct our key signatures using the circles, we generate 30 key signatures (28 from the circles and Cmaj/Cmin). The solution is to ignore a few of the redundant keys. Personally, I prefer B major over Cb Major because 5 sharp accidentals is easier to work with than 7 flat accidentals. The reverse is true for Db and C#. in the case of Gb and F#, we have the exact same number of accidentals, and using either key forces us to think of either "F" as "E Sharp" or "B" as "C Flat." Whatever key we choose, we can at least recognize that the notes will be the same, The only thing that differs is how we choose to think about them.

In music theory, we can contemplate, organize, and construct whatever methods and categories we wish, but in the end, we'd be wise to remember that we are dealing with frequencies and the mathematical relationships between them.

So, what can we do with our major scales and key signatures? For one, we can build diatonic chords, chords that work within our key signature. For each note in our scale, we can build a chord triad using the root, a third, and a fifth. The thirds and fifths we use are predetermined by our scale, and thus, for each position in our scale, the qualities of each chord are also predetermined.

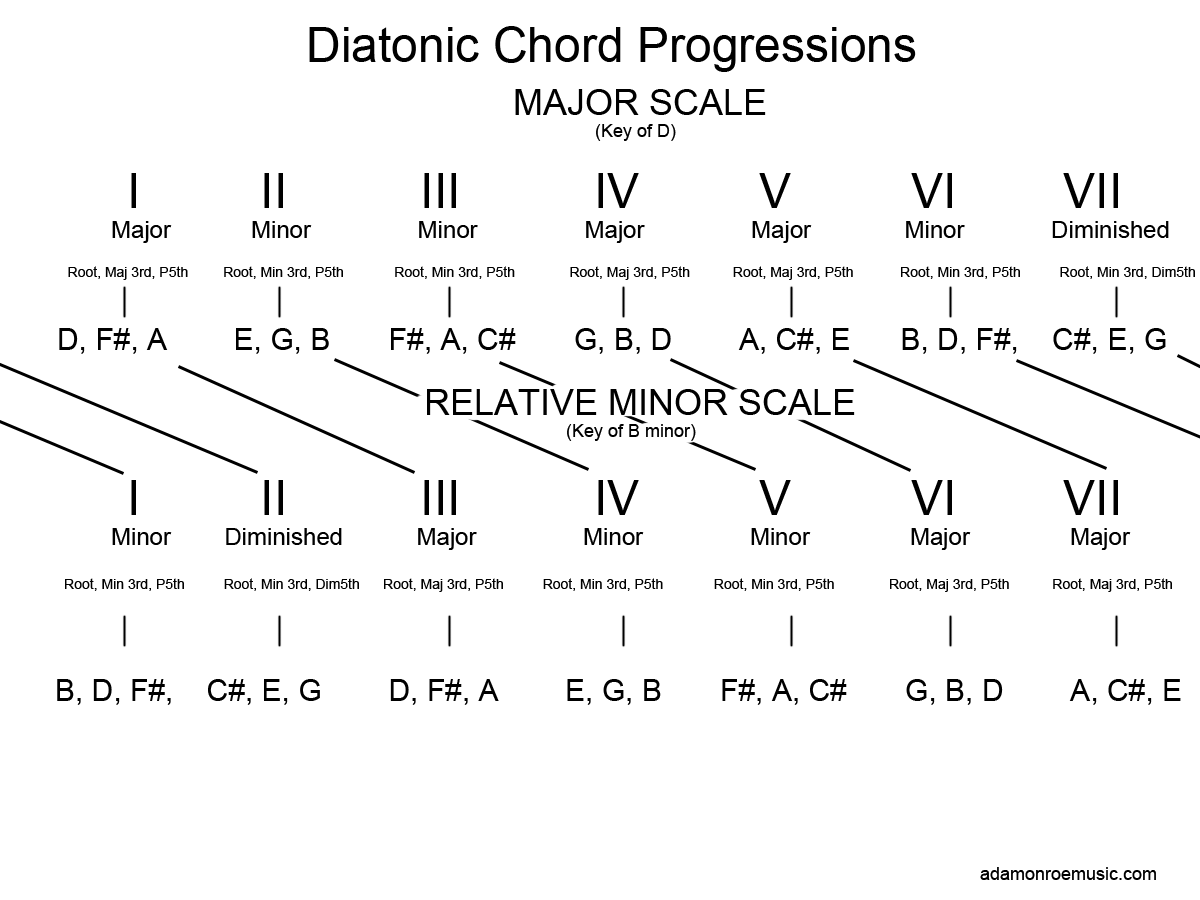
Chords diatonic to a major key are as follows: I:Major, II:Minor, III:Minor, IV:Major, V:Major, VI:Minor, VII:Diminished. We use Roman numerals to denote each chord, because it makes it easier to think about music in terms of chord progressions, and not just in terms of specific chords. Some chord progressions have become extremely popular over the history of music, such as the I-IV-V progression, the I-VI-IV-V progression, and the blues progression.

Let us examine diatonic chords in the key of D. To construct a D major chord, we use the notes D, F#, and A. These are, of course, the major third and perfect fifth from the D major scale. To construct the IV chord, we use the notes G, B, and D. Not surprisingly, these are the major third and perfect fifth of the G major scale, but they are also notes diatonic to the key of D. Regarding minor chords, the III chord is a F# minor chord, because F#, A, C# follow the F# minor scale, and also adheres to the notes of the D major scale. The VII chord contains the notes C#, E, and G, because, in order to work with our 7 D major notes, we must use the minor 3rd of C#, as well as flatten the perfect fifth (G#), which becomes G, the interval of a diminished fifth.

Diatonic chords in a minor key are as follows: I:Minor, II:Diminished, III:Major, IV:Minor, V:Minor, VI:Major, VII:Major. This is because, if we consider the relative minor scale as starting on the VI of the relative major scale, then we are really only beginning in a different place of the major scale chord progression and cycling back through that progression.

Triads are not the only type of chords that exist. In our next lesson, we will discuss 7th, 9th, 11th, and 13th chords, inversions, blue notes, and scales other than the major, such as the pentatonic.