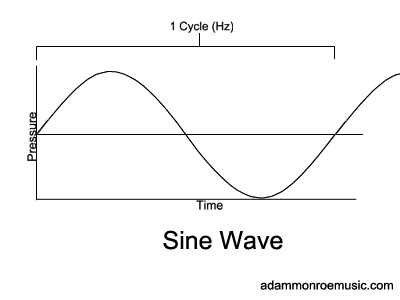In order to talk about music, we must first discuss sound. What is sound? Sound is the movement (vibration) of particles in a medium (such as air or water) caused by longitudinal waves of contracting and expanding pressure. You can't jam-out on a guitar in space, because space is a vacuum and lacks a medium in which waves can propagate. We can think about this musically in terms of something like a guitar string; when you pluck a guitar string, the string vibrates, creating areas of high and low-pressure. We can represent these waves mathematically as sine waves, but we must be careful to note that pure sine waves don't really exist in nature, because sound tends to be comprised of multiple frequencies, as well as things like harmonics, which combine to produce complex waveforms. We can record changes in sound pressure as discrete time signals (digital sampling) or as analog signals in a physical medium (vinyl records, magnetic tape, ect.) and reproduce these sounds by vibrating physical objects - typically the cones found inside of speakers. We measure the frequency (or pitch) of sound in Hertz (Hz), or (wave) cycles-per-second. In other words, how many times a wave completes a cycle of compression and rarefaction per second determines the perceived pitch, and waves with more cycles sound "higher," well those with fewer cycles sound "lower." Because sound travels at a somewhat fixed velocity (the speed of sound varies by temperature and medium, approximately 1,126 ft/second at 68 degrees Fahrenheit in open-air), frequency is inversely proportional to wavelength. In other words Frequency=Speed of Sound/Wavelength. For example, a 440 Hz tone has a wavelength of 2.56 ft because 1126 ft/second divided by 440 is roughly equal to 2.56. A much lower tone, say 20Hz (at the floor of human hearing) has a much longer wavelength of 56.3 ft!

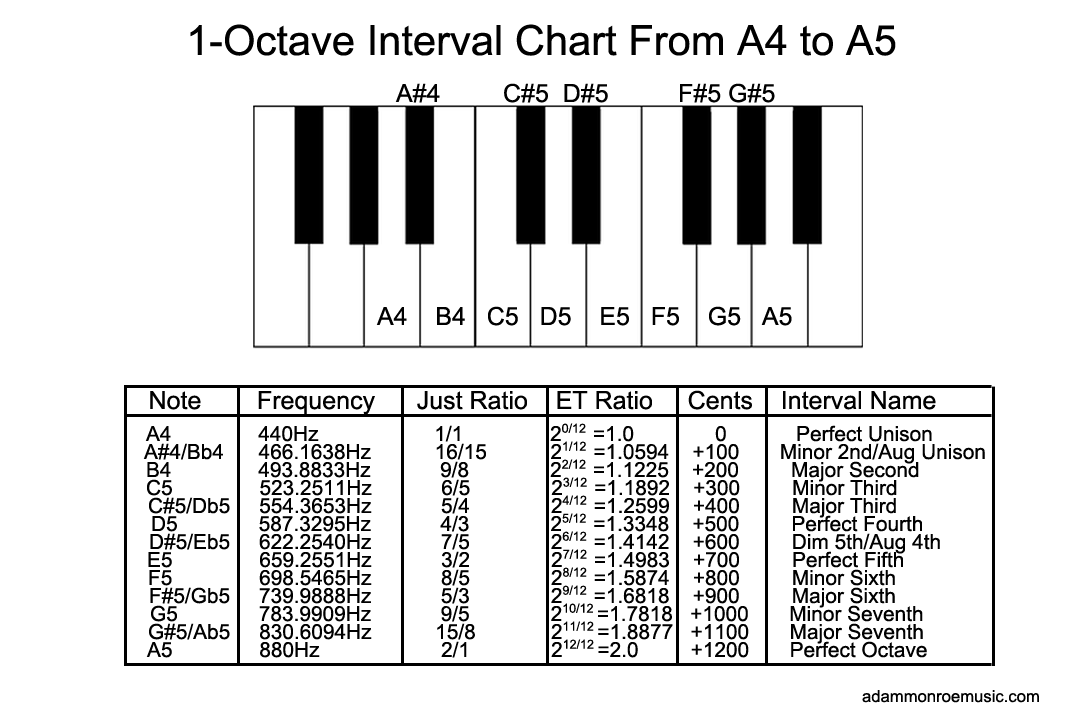
Riveting stuff to be sure, but how does it relate to music? At it's core, music is mathematics. We have determined that individual pitches in music correspond to the frequency of a wave's cycle, and indeed, in the modern twelve-tone system we have given many of these frequencies names. For example, A4 (the first A above C4 on a piano) is typically tuned to 440 Hz, but this is a somewhat arbitrary convention, because in music we aren't that concerned with absolute frequencies, but rather, the relationship between those frequencies, called intervals. A4 has been tuned to 432 Hz and 435 Hz in the past, and some people still use alternate A4 tunings, but for the sake of simplicity will use 440 Hz in our examples. Our modern 12-tone equal-temperament tuning system is based on a set of 12 equally-spaced intervals, but what is an interval? A musical interval is the distance between two frequencies, but to really understand this relationship, we have to go beyond 12-tone equal temperament and look at another system of tuning called just intonation. In just intonation intervals are tuned to true mathematical ratios, based on a root note. The interval between two notes of the same pitch, one higher and one lower, is called an octave, and it is a 2/1 ratio, the higher pitch being doubling the frequency of the lower pitch. Using A4 440Hz as an example, A5 is 880 Hz, A6 is 1760 Hz, A3 is 220 Hz, ect. If you play A4 and A5 together, the two notes will sound harmonious, pleasant, and stable, because 2/1 is a simple, stable mathematical ratio. Continuing in just intonation, the ratio between A and E is a 3/2 ratio (or 1.5) so with A4 tuned to 440Hz, "just" E5 is 660Hz. In equal temperament tuning, the equivalent frequency is 659.26 Hz, just slightly off a perfect ratio. 3/2 is another stable, pleasant ratio, not as pleasant or as stable sounding as 2/1, but a pretty nice place to begin building a musical chord (three or more notes played at once.) In music we refer to this interval as the perfect fifth. As we continue building intervals in just intonation, we come across more pleasant ratios like the major third (5/4) and the perfect fourth (4/3) and less pleasant ones, like the major 7th (15/8) and the minor second (16/15).

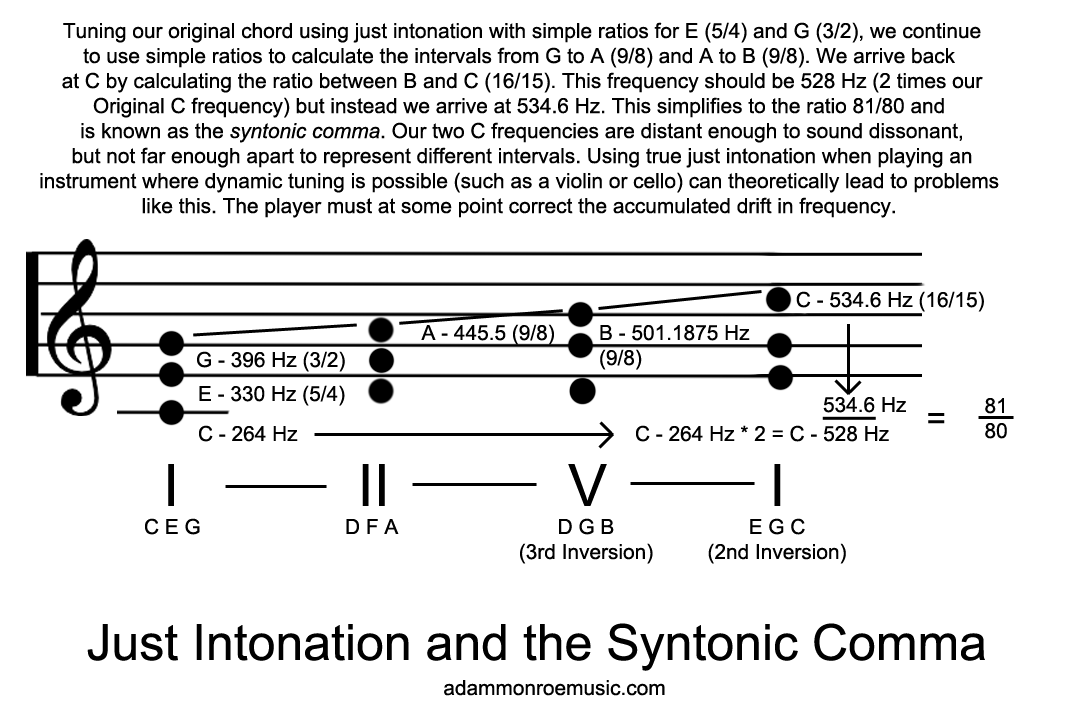
If the intervals in just intonation are mathematically perfect ratios, why do we use "imperfect" equal-temperament tuning? Because Just intonation can only really sound good in one key at a time without needing to be retuned, and even then, some chords won't be pure (major chords sound fine, minor chords deviate from simple ratios). For example, in a scale justly tuned to C, a D minor chord will contain the notes D, F, and A. The F (the interval of a minor third) would require a 6/5 ratio (1.2) to be "just," but the ratio will end up being 32/27 (1.185) because we have based our tuning off of the C frequency, not D. The A (the interval of a perfect fifth) should be a 3/2 ratio (1.5) but ends up being 40/27 (1.481). The difference between the "C" tuned A and the "D" tuned A is 21 cents - we will discuss cents later. We can correct these differences by slightly adjusting the pitch if we are playing a fretless instrument like a violin, but when using fixed-pitched instruments like fretted guitars and pianos, we are stuck with these errors. However, even when we are able to theoretically correct these errors by adjusting pitch so that all of our intervals remain pure, playing a simple chord progression like I - II - V - I with inverted chords and just ratios will bring us back to a C that is not the same as the one we started with, being an81/80 ratio or 0.012% different. This is known as the syntonic comma, and will sound out-of-tune. Other systems of tuning have been used - such as Pythagorean where notes are built from perfect fifths (3/2 ratio) starting with a root note, for example C G D A E B F# C# G# Eb Bb F - but all tuning systems based on pure ratios will create at least a few dissonant/incorrect intervals (and wolf notes), and thus, limit modulation when used, and sometimes even the use of simple chords.

Equal temperament tuning addresses these issues by spreading-out these tuning errors equally. As its name implies, the distances between all semitones become equal. A semitone is the smallest interval in western music, and corresponds directly to the distance between adjacent keys on a piano, or adjacent frets on a guitar. The distance of a semitone is 100 cents. A cent isn't a unit of measurement in the traditional sense, it is more of a logarithmic function, but useful as a concept, because it allows us to prove that semitones are equal, and that an octave spans 1200 cents. Therefore we can say that a perfect fifth is no longer a 3/2 ratio, but rather, that it spans 700 cents. We can check this with a logarithmic formula. Going back to our old friend 440 A, we know that the perfect fifth of A is E, and in equal temperament it is 659.255 Hz - we'll discuss how we arrive at this frequency in a moment. Knowing these two frequencies, we can check the cents between them with the function N=1200 * log2 (b/a) where b and a represent our two known frequencies. 659.255/440 = 1.49830. log2(1.49839) = 0.583326 * 1200 =699.9912 or about 700 cents (we have been rounding our decimals down.) Now interestingly, note that 1.49830 is pretty close to our simple ratio of 3/2 (1.5) Indeed, most of our equal temperament ratios only deviate from their pure just ratio analogues by 1% or less, and in the case of the perfect fifth and perfect fourth, the difference is a mere 0.1%. Going back to 440 A, how did we calculate the 659.255Hz E? We used the twelfth root of two, generally credited to French mathematician Marin Mersennne. The twelfth root of 2 is 2 to the power of 1/12, or 1.059453. But how to calculate E? By definition we know that a perfect fifth is 700 cents away from the root, or 700/1200, or 2 to the power of 7/12 or 2 to the power of 0.5833333 gives us 1.4983070768. 440Hz * 1.4983070768 gives us 659.255Hz, or equal temperament E. In equal temperament tuning, we can define all of our interval ratios by determining the cent difference in increments of 100. The nice thing about equal temperament is that in any key, our intervals will always be calculated the same way. Apart from the octave, no ratio will be a perfect simple ratio, but neither will we have a few "perfect" ratios mixed with a few "imperfect" ones, and we can easily transpose and modulate to different musical keys without having to worry about notes sounding off. The disadvantage is that, because no ratios are perfect (with the exception of the octave) we will hear musical beating more distinctly then in other tuning systems. However, modern ears have gotten fairly used to this.

Another question we might ask ourselves is why a 12-tone system? Why not 24 or 8? Mostly trial-and-error, but consider this: the 12-tone system is the smallest system that contains close approximations of the important consonant intervals. What are consonant intervals? Consonance is a somewhat subjective term, but basically, most of the intervals we have already discussed and their corresponding simple ratios - 6/5, 5/4, 4/3, 3/2, 8/5, and 5/3 or the minor third, major third, perfect fourth, perfect fifth, minor sixth, and major sixth are consonant intervals. We could use a 19-tone ET scale and many of the intervals would be closer to pure ratios, but the perfect fifth and perfect fourth would sound worse. We could use a 53-note ET scale and the intervals would sound better, but 53 notes is not very practical. Incidentally, 12 tones also come close to matching the number of fingers we have.

Why are intervals so important? Because music theory is based on intervals. Chords, progressions, and melody all derive from the idea of mathematical intervals. The frequencies themselves are almost irrelevant. If you take a musical recording and speed it up slightly, or slow it down depending on the amount, you will sometimes change the pitch of the music so that it sits in-between proper keys - all the notes will be, say, 24 cents higher than they should be, but this will not sound bad, because the mathematical ratios haven't changed. Unless you have perfect pitch, you probably won't even notice the difference unless you attempt to pick out notes on a standard tuned instrument. This is done all the time, the song "Layla" being a prime example.

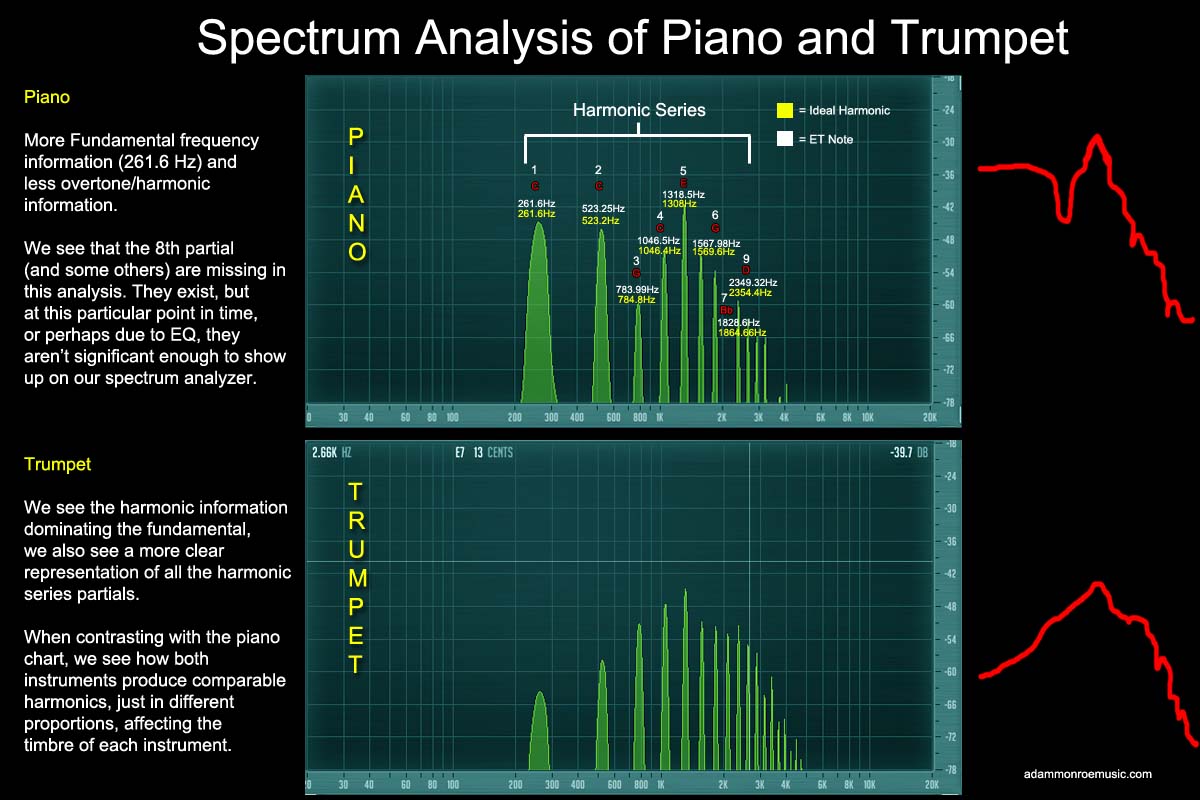Up until now, we've mostly dealt with the idea of musical pitches by discussing their fundamental frequencies (for example 440 A) but musical sounds also contain harmonic information, because things like strings don't vibrate at just one frequency, but rather, several frequencies at once that combine to form complex tones. The overtones that a musical instrument produces in proportion to their fundamental frequency determine the timbre of the instrument. "smoother" sounds like violins tend to contain less prominent harmonics and overtones, well more "harsh" sounding instruments like brass have more prominent harmonics. Harmonics are multiples of the fundamental frequency, I.E., 2/1, 3/1, 4/1, 5/1, 6/1, 7/1 ect. These pure ideal harmonics may or may not match the real harmonic partials of an instrument, but they usually come close. The harmonics of 440 A are 440, 880, 1320, 1760, 2200, 2640, 3080, 3520, and a few more. These correspond to the musical pitches A, A, E, A, C#, E, G, and A. We could sum-up the first 7 partials of the harmonic series as the following intervals: octave, perfect fifth, perfect fourth, major third, minor third, minor third, perfect second, although some of these harmonics deviate quite a bit from equal temperament, especially the 7th partial. If you lightly touch a harmonic node on a fretted instrument like a guitar (for example, above the 12th fret) you can stop the fundamental note from sounding and hear the harmonic. On a trumpet, you can control the speed of air flow to produce higher and higher harmonic partials.

In our next lesson, we'll learn how to build scales, key signatures, and major and minor chords using our system of intervals, and we'll also discuss the cycle of fourths and the cycle of fifths.